Chapter 10 Additional programming concepts

Learning Objectives

Learn programming concepts, including

  • how to handle conditions
  • iteration of data structures
  • good coding practice
  • code re-use through functions

When the size and the complexity of the data increases, or the data science question of interest becomes more complex, the data analysis techniques as we have seen them so far need to be complemented with programming techniques. From a data science point of view, there is no clear delimitation between data analysis and (data) programming, both morphing into each other19.

This chapter will introduce some additional programming skills and demonstrate how to use them in the context of high troughput omics data.

10.1 Writing clean code

Writing clean code means writing easily readable code, hence easily understandable code and, eventually code with less bugs. One easy way to achieve this is through consistency, i.e. stick to a style guide. The issue is that there are several style guides available, often with conflicting suggestions. Two widely used ones are the Bioconductor style guide and Hadley Wickhams’s R Style Guide. The advice from for naming variables seen in the first and second chapters are also relevant.

Here are a couple of suggestions:

  • Use <- to assign variables. Use = is also valid, but make sure that you stick with one.
  • Use either camel case (camelCaseNaming) of snake case (snake_case_naming), and avoid using dots (don’t use dot.variable.names). These conventions apply to functions, variables and files (for the latter, a - instead of _ is also acceptable).
  • Always spell out TRUE and FALSE, and resist the temptation to use T and F instead20.
  • Use 4 spaces for indenting. No tabs.
  • No lines longer than 80 characters.
  • Use spaces around binary operators.
  • No spaces between a function name and the opening parenthesis.

Another good advise is to avoid re-writing the same code many times. We will see below two strategies to do that, namely iteration and writing new functions. This firstly reduces the amount of code typed and hence the number of bugs, but more importantly enables consistency. If something in your code changes, there’s only one change and it applies everywhere, rather than doing that same change repeatedly (at the first of adding bugs and to miss some updates).

When writing code, keep it simple and short21. Ideally, the code should be evident. But when the questions tackled are not trivial, is becomes essential to add comments to clarify aspects of the script/program. Make sure to use them to describe why something is done, rather than explaining how things are done (which is tyically best done by the code itself).

A general guideline to avoid bugs is to apply defensive programming:

  • making the code work in a predicable manner
  • writing code that fails in a well-defined manner
  • if something weird happens, either properly deal with it, or it fail quickly and loudly

Here are some examples of how to do this:

  • use functions like is.numeric(x), is.character(x), is.data.frame(x), … but make sure that the variable you are going to use is of the expected type.

  • Make sure the length or dimensions of what you are going to use are what you expect:

length(x) > 0
nrow(x) > 0
ncol(x) > 0
  • Failing fast and well! Wrap such test in stopifnot(), so that if they fail, you get immediately an error, rather than risking that you code fails later with obscure error messages or, worse, the code runs to completion but returns meaningless results.
stopifnot(length(x) > 0)
stopifnot(dim(x) > 0) ## same as next one
stopifnot(ncol(x) > 0, nrow(x) > 0)

10.2 Iteration

Iteration describes the situtation when a specific operation has to be repeated many times on different inputs of the same type. For example, if we have a vector of numeric x shown below,

(x <- 1:10)
##  [1]  1  2  3  4  5  6  7  8  9 10

and we wanted to apply the logarithm operation on each element of x, it wouldn’t be convenient to type

log(1)
log(2)
log(3)
...
log(10)

The concept of iteration allows us to program the following command:

Repeat log for each value of my input x.

or more formally

Repeat log(i) where i takes in turn each value of my input x.

We will see different ways of implementing such an iteration.

Using a for loop

for (i in x) {
    print(log(i))
}
## [1] 0
## [1] 0.6931472
## [1] 1.098612
## [1] 1.386294
## [1] 1.609438
## [1] 1.791759
## [1] 1.94591
## [1] 2.079442
## [1] 2.197225
## [1] 2.302585

The loop above only prints the results on screen. They aren’t stored and are lost for any further re-use, which would be very annoying if it took much more time to perform all the calculations. In the code chunk below, we are going to first inititalise a vector with the appropriate number of NA values and, at each iteration, we then store the result. We however now need to change our loop and iterate of the indices of the input vector, so that we can re-use these indices to save the results in the output vector.

res_loop <- rep(NA, length(x))
for (i in seq_along(x)) {
    res_loop[i] <- log(x[i])
}
res_loop
##  [1] 0.0000000 0.6931472 1.0986123 1.3862944 1.6094379 1.7917595 1.9459101
##  [8] 2.0794415 2.1972246 2.3025851

Using the apply function

The apply family of functions implements our defintion of iteration quite literally

Repeat log for each value of my input x

is reformulated as

For each value of my input x, apply log

and coded as

res_apply <- sapply(x, log)
res_apply
##  [1] 0.0000000 0.6931472 1.0986123 1.3862944 1.6094379 1.7917595 1.9459101
##  [8] 2.0794415 2.1972246 2.3025851

There are three such function that apply a function iteratively:

  • sapply iterates over a vector and returns a new vector of the same length as the input vector22.

  • lapply iterates over a linear input (a vector of a list) and returns a list of the same length as the input.

  • apply iterates of the rows or the columns of a data.frame or matrix and returns a list or vector or approritate length (number of rows or columns). The dimension over which the iterations proceeds is defined by the second argument, where 1 defines rows and 2 defined columns23.

When performing the same operations in different ways (using different implementations), it is essential to verify that the results are identical or, if not, at least compatible. The most direct way to do the former is to use the identical function:

identical(res_loop, res_apply)
## [1] TRUE

The purrr package a set of map functions similar to the apply set described above.

Vectorisation

We must not forget the obvious, which is vectorisation. Many R functions work by default iteratively on every element of a vectors, i.e. they work irrespectively whether the vector is of length 124 or longer.

res_vec <- log(x)
res_vec
##  [1] 0.0000000 0.6931472 1.0986123 1.3862944 1.6094379 1.7917595 1.9459101
##  [8] 2.0794415 2.1972246 2.3025851

And, as before, we check that we obtain identical results:

identical(res_loop, res_vec)
## [1] TRUE

Which iteration to use?

Even though they produce the same result, the iteration strategies above aren’t equal, and some should be preferred in different situations.

  • When a vectorised solution exists, this is the one that should be chosen. It is by far the fastest solution, but only applicable to existing vectorised functions. If you were to write your own function to iterate over, it is advisable to write a vectorised function.

  • The apply functions are extremely convenient and concise, and hence widely used. They have a couple of advantages, including that there is no need to explicitly initialise a result variable and that they can easily be parallelised.

  • For loops are the most generic solution for iteration, and they require to initialise the result variable that will be populated during the loop. As opposed to popular belief, they aren’t slower than using apply functions. They are however the best solution if, during the iteration, one has the access another element than the one currently processed (typically, if i is the counter, accessing i + 1 or i - 1).

► Question

Use the expressions.csv() function from the rWSBIM1207 package to get the path to 5 csv files containing gene expression data for a single gene and hundreds of patience. Read all data in and combine them into a single dataframe.

Before starting, open at least two of these files to familiarise yourself with their structure and identify how and with what function they need to be combined.

► Solution

10.3 Conditionals

When an operation has to be executed when a condition is met, one typically uses a if and else construct:

if (CONDITION) {
   ## DO SOMETHING
} else {
  ## DO SOMETHING ELSE
}

For examples

(x <- rnorm(1))
## [1] -0.6264538
if (x > 0) {
   print(log(x))
} else {
   print(log(-x))
}
## [1] -0.4676802

But note that in the example above, it would be much better to simplify the code and use the absolute value of x before taking the log, which will generalise the calculation for positive and negative values …

log(abs(x))
## [1] -0.4676802

… and works for vectors of any length thanks to vectorisation.

x <- rnorm(10)
log(abs(x))
##  [1] -1.6947599 -0.1795710  0.4670498 -1.1101553 -0.1978799 -0.7186105
##  [7] -0.3033716 -0.5520273 -1.1861709  0.4132885

There are also in-line, vectorised versions of the if/else statements seen above: the ifelse function that ships with the base package, and if_else from dplyr. Both work similarly (the differences are beyond the scope of this course) and have the form:

if_else(condition, true, false)
  • where condition is the condition to be tested, and will return either TRUE or FALSE;
  • true is the expression that is executed if the condition is TRUE;
  • false is the expression that is executed otherwise (i.e if the condition is FALSE).

Here is an example, that will return 1 if x is strictly positive, and 0 otherwise:

x <- 0.5
if_else(x > 0, 1, 0)
## [1] 1

The function being vectorised, the condition can be a vector of length greater than 1:

x <- rnorm(10)
x
##  [1]  0.38984324 -0.62124058 -2.21469989  1.12493092 -0.04493361 -0.01619026
##  [7]  0.94383621  0.82122120  0.59390132  0.91897737
if_else(x > 0, 1, 0)
##  [1] 1 0 0 1 0 0 1 1 1 1

The vectorised conditional functions can directly be used in a standard data analysis pipeline:

x <- tibble(x = letters[1:5],
            y = rnorm(5))
x
## # A tibble: 5 × 2
##   x          y
##   <chr>  <dbl>
## 1 a     -0.626
## 2 b      0.184
## 3 c     -0.836
## 4 d      1.60 
## 5 e      0.330
mutate(x, z = if_else(y > 0, 1, 0))
## # A tibble: 5 × 3
##   x          y     z
##   <chr>  <dbl> <dbl>
## 1 a     -0.626     0
## 2 b      0.184     1
## 3 c     -0.836     0
## 4 d      1.60      1
## 5 e      0.330     1

10.4 Writing new functions

A function is composed of a name, inputs (inside the parenthesis), a body (between curly brackets) and an ouput (last statement or variably inside the return statement).

my_fun <- function(x, y) {
    message("First input: ", x)
    message("Second input: ", y)
    z <- x * abs(y)
    return(z)
}
my_fun(2, -5)
## First input: 2
## Second input: -5
## [1] 10

► Question

Complete the following function. It is supposed to take two inputs, x and y and, depending whether the x > y or x <= y, it generates the permutation sample(x, y) in the first case or draws a sample from rnorm(1000, x, y) in the second case. Finally, it returns the sum of all values.

fun <- function(x, y) {
    res <- NA
    if (   ) {
        res <- sample(, )
    } else {
        res <- rnorm(, , )
    }
    return()
}

To check your answer, run it with inputs 5, 15 and 15, 5, after setting the random number generator to 1 each time with set.seed(1) and you should get 4825.2778709 and 23.

► Solution

10.5 Pattern matching

One skill that comes handy more often than not is the ability to find patterns in text and replace these. We are going to see two functions out of many to perform such tasks. As an illustration, we are going to mine a vector or peptides identified by mass spectrometry. The data can be loaded from the rWSBIM1207 data:

library("rWSBIM1207")
data(peptides)
length(peptides)
## [1] 26796
head(peptides)
## [1] "aAAGEAk" "VTEEAk"  "aSGDPGk" "sAAAEAk" "aANAEGk" "aAAEEAR"
  1. Among the 26796 petides, which ones contain the pattern "AAGE"?
pattern <- "AAGE"
## indices of matching peptides
grep(pattern, peptides)
## [1]     1  7026 17140 21912 23423 24947 25257 26658
## matching peptides
grep(pattern, peptides, value = TRUE)
## [1] "aAAGEAk"              "aFHGAAGEAGAAFGNHGANR" "eAIDAAGEGGR"         
## [4] "sAAGEFADDPcSSVkR"     "eAAGEGPVLYEDPPDQk"    "eIEAAGEk"            
## [7] "dVQELYAAGENR"         "sAAGEFADDPcSSVk"
## position of matching peptides
head(grepl(pattern, peptides))
## [1]  TRUE FALSE FALSE FALSE FALSE FALSE
  1. Replace a pattern by another string.
head(peptides)
## [1] "aAAGEAk" "VTEEAk"  "aSGDPGk" "sAAAEAk" "aANAEGk" "aAAEEAR"
head(sub("AE", "XX", peptides))
## [1] "aAAGEAk" "VTEEAk"  "aSGDPGk" "sAAXXAk" "aANXXGk" "aAXXEAR"

But careful that sub only replaced the first occurrence in a string!

head(peptides)
## [1] "aAAGEAk" "VTEEAk"  "aSGDPGk" "sAAAEAk" "aANAEGk" "aAAEEAR"
head(sub("A", "X", peptides))
## [1] "aXAGEAk" "VTEEXk"  "aSGDPGk" "sXAAEAk" "aXNAEGk" "aXAEEAR"
head(gsub("A", "X", peptides))
## [1] "aXXGEXk" "VTEEXk"  "aSGDPGk" "sXXXEXk" "aXNXEGk" "aXXEEXR"

10.6 Analysing data from multiple files

This exercise recapitulates the most important material that we have seen in this course. We are going to analyse the student tests A and B results using functionality from the dplyr package (seen in chapter 5). The student test files are available in the rWSBIM1207 package (the interroA.csv and interroB.csv functions return their respective paths). We want to compare how the male and female students in groups A and B have performed. To do this, we want to calculate the mean scores and visualise the score distributions in each groups.

► Question

Before writing any code to answer the questions above, take a couple of minutes to think about what packages are needed to answer the questions above and identify the individual steps needed to first prepare the data needed to find the answers and then to produce the answers.

  1. Start by loading the rWSBIM1207 and tidyverse package, to get all the functionality we will need.

► Solution

  1. Using the interroA.csv() and interroB.csv() functions from the rWSBIM1207 package, create a vector containing the two csv file names.

► Solution

  1. Iterate over the files and read each into an element of a list. Then, bind the two elements of the list into a single dataframe containing all results.

► Solution

  1. What are the mean scores for male and female students in each test (interro1 to interro4).

► Solution

  1. What are the mean scores for male and female students in each test (interro1 to interro4) and in each group (A and B).

► Solution

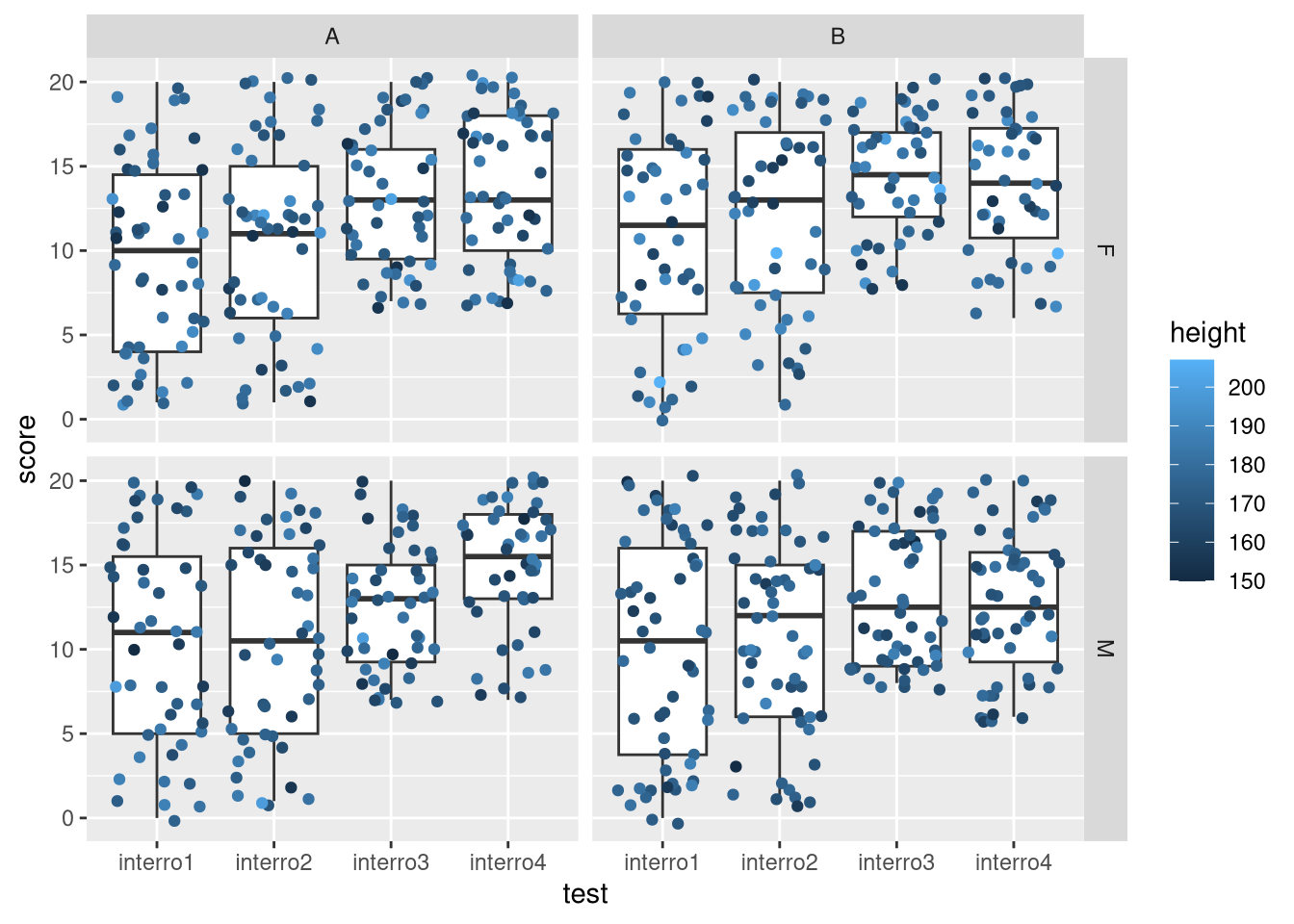
  1. Instead of comparing the means for the four tests in each group and gender, visualise their distributions using boxplots. In addition to the boxplots, overlay the actual score values (using the jitter geom) and colour the points based on the students height.

► Solution

10.7 Additional exercises

► Question

Complete the following function that converts meters to yards, knowing that that 1 yard corresponds to 0.9144 meters

meters_to_yards <- function(argument goes here) {
  yards <- _code goes here!_
  return(yards)
}

► Question

Write functions that convert temperatures:

  • from Fahrenheit to Kelvin, where \(T_K = (T_F - 32) \times 5/9 + 273.15\)
  • fom Celsius to Kelvin, where \(T_K = T_C + 273.15\)
  • from Kelvin to Celsis
  • from Fahrenheit to Celsius

  1. A fundamental difference however is how data analysis and programming are taught. When it comes to researchers, and biomedical researchers in particular, teaching programming to analyse data isn’t successful. Teaching data analysis to eventually programme with data, however, has proven a successful strategy.↩︎

  2. TRUE and FALSE are reserved words; one can’t use them as variable names. This however doesn’t hold for T and F. One can use T and F as regular variable names such, as for example, T <- FALSE and F <- TRUE!↩︎

  3. The official motto is KISS, keep your functions simple, stupid, widely used in programming.↩︎

  4. This is a simplification of how sapply works, that is partly defined by the the simplify argument and whether the result of applying the function on each element of the input can be returned as a vector. The alternative is to return a list, like lapply.↩︎

  5. This generalises to arrays with more than 2 dimensions.↩︎

  6. A vector of length 1 would be called a scalar in other programming languages.↩︎

Page built: 2024-03-15 using R version 4.3.2 Patched (2023-12-27 r85757)