Chapter 3 Introduction to R

Learning Objectives

  • Define the following terms as they relate to R: object, assign, call, function, arguments, options.
  • Assign values to objects in R.
  • Learn how to name objects
  • Use comments to inform script.
  • Solve simple arithmetic operations in R.
  • Call functions and use arguments to change their default options.
  • Inspect the content of vectors and manipulate their content.
  • Subset and extract values from vectors.
  • Analyse vectors with missing data.

3.1 Creating objects in R

You can get output from R simply by typing math in the console:

3 + 5
## [1] 8
12 / 7
## [1] 1.714286

However, to do useful and interesting things, we need to assign values to objects. To create an object, we need to give it a name followed by the assignment operator <-, and the value we want to give it:

weight_kg <- 55

<- is the assignment operator. It assigns values on the right to objects on the left. So, after executing x <- 3, the value of x is 3. The arrow can be read as 3 goes into x. For historical reasons, you can also use = for assignments, but not in every context. Because of the slight differences in syntax, it is good practice to always use <- for assignments.

In RStudio, typing Alt + - (push Alt at the same time as the - key) will write <- in a single keystroke in a PC, while typing Option + - (push Option at the same time as the - key) does the same in a Mac.

Naming variables

Objects can be given any name such as x, current_temperature, or subject_id. You want your object names to be explicit and not too long. They cannot start with a number (2x is not valid, but x2 is). R is case sensitive (e.g., weight_kg is different from Weight_kg). There are some names that cannot be used because they are the names of fundamental functions in R (e.g., if, else, for, see here for a complete list). In general, even if it’s allowed, it’s best to not use other function names (e.g., c, T, mean, data, df, weights). If in doubt, check the help to see if the name is already in use. It’s also best to avoid dots (.) within an object name as in my.dataset. There are many functions in R with dots in their names for historical reasons, but because dots have a special meaning in R (for methods) and other programming languages, it’s best to avoid them. It is also recommended to use nouns for object names, and verbs for function names. It’s important to be consistent in the styling of your code (where you put spaces, how you name objects, etc.). Using a consistent coding style makes your code clearer to read for your future self and your collaborators. In R, some popular style guides are Google’s, the tidyverse’s style and the Bioconductor style guide. The tidyverse’s is very comprehensive and may seem overwhelming at first. You can install the lintr package to automatically check for issues in the styling of your code.

Objects vs. variables What are known as objects in R are known as variables in many other programming languages. Depending on the context, object and variable can have drastically different meanings. However, in this lesson, the two words are used synonymously. For more information see: https://cran.r-project.org/doc/manuals/r-release/R-lang.html#Objects

When assigning a value to an object, R does not print anything. You can force R to print the value by using parentheses or by typing the object name:

weight_kg <- 55    # doesn't print anything
(weight_kg <- 55)  # but putting parenthesis around the call prints the value of `weight_kg`
## [1] 55
weight_kg          # and so does typing the name of the object
## [1] 55

Now that R has weight_kg in memory, we can do arithmetic with it. For instance, we may want to convert this weight into pounds (weight in pounds is 2.2 times the weight in kg):

2.2 * weight_kg
## [1] 121

We can also change an object’s value by assigning it a new one:

weight_kg <- 57.5
2.2 * weight_kg
## [1] 126.5

This means that assigning a value to one object does not change the values of other objects. For example, let’s store the animal’s weight in pounds in a new object, weight_lb:

weight_lb <- 2.2 * weight_kg

and then change weight_kg to 100.

weight_kg <- 100

► Question

What do you think is the current content of the object weight_lb? 126.5 or 220?

3.2 Comments

The comment character in R is #, anything to the right of a # in a script will be ignored by R. It is useful to leave notes, and explanations in your scripts.

RStudio makes it easy to comment or uncomment a paragraph: after selecting the lines you want to comment, press at the same time on your keyboard Ctrl + Shift + C. If you only want to comment out one line, you can put the cursor at any location of that line (i.e. no need to select the whole line), then press Ctrl + Shift + C.

► Question

What are the values after each statement in the following?

mass <- 47.5            # mass?
age  <- 122             # age?
mass <- mass * 2.0      # mass?
age  <- age - 20        # age?
mass_index <- mass/age  # mass_index?

3.3 Functions and their arguments

Functions are “canned scripts” that automate more complicated sets of commands including operations assignments, etc. Many functions are predefined, or can be made available by importing R packages (more on that later). A function usually gets one or more inputs called arguments. Functions often (but not always) return a value. A typical example would be the function sqrt(). The input (the argument) must be a number, and the return value (in fact, the output) is the square root of that number. Executing a function (‘running it’) is called calling the function. An example of a function call is:

b <- sqrt(a)

Here, the value of a is given to the sqrt() function, the sqrt() function calculates the square root, and returns the value which is then assigned to the object b. This function is very simple, because it takes just one argument.

The return ‘value’ of a function need not be numerical (like that of sqrt()), and it also does not need to be a single item: it can be a set of things, or even a dataset. We’ll see that when we read data files into R.

Arguments can be anything, not only numbers or filenames, but also other objects. Exactly what each argument means differs per function, and must be looked up in the documentation (see below). Some functions take arguments which may either be specified by the user, or, if left out, take on a default value: these are called options. Options are typically used to alter the way the function operates, such as whether it ignores ‘bad values’, or what symbol to use in a plot. However, if you want something specific, you can specify a value of your choice which will be used instead of the default.

Let’s try a function that can take multiple arguments: round().

round(3.14159)
## [1] 3

Here, we’ve called round() with just one argument, 3.14159, and it has returned the value 3. That’s because the default is to round to the nearest whole number. If we want more digits we can see how to do that by getting information about the round function. We can use args(round) or look at the help for this function using ?round.

args(round)
## function (x, digits = 0, ...) 
## NULL
?round

We see that if we want a different number of digits, we can type digits=2 or however many we want.

round(3.14159, digits = 2)
## [1] 3.14

If you provide the arguments in the exact same order as they are defined you don’t have to name them:

round(3.14159, 2)
## [1] 3.14

And if you do name the arguments, you can switch their order:

round(digits = 2, x = 3.14159)
## [1] 3.14

It’s good practice to put the non-optional arguments (like the number you’re rounding) first in your function call, and to specify the names of all optional arguments. If you don’t, someone reading your code might have to look up the definition of a function with unfamiliar arguments to understand what you’re doing.

3.4 Vectors and data types

A vector is the most common and basic data type in R, and is pretty much the workhorse of R. A vector is composed by a series of values, which can be either numbers or characters. We can assign a series of values to a vector using the c() function. For example we can create a vector of animal weights and assign it to a new object weight_g:

weight_g <- c(50, 60, 65, 82)
weight_g
## [1] 50 60 65 82

A vector can also contain characters:

molecules <- c("dna", "rna", "protein")
molecules
## [1] "dna"     "rna"     "protein"

The quotes around “dna”, “rna”, etc. are essential here. Without the quotes R will assume there are objects called dna, rna and protein. As these objects don’t exist in R’s memory, there will be an error message.

There are many functions that allow you to inspect the content of a vector. length() tells you how many elements are in a particular vector:

length(weight_g)
## [1] 4
length(molecules)
## [1] 3

An important feature of a vector, is that all of the elements are the same type of data. The function class() indicates the class (the type of element) of an object:

class(weight_g)
## [1] "numeric"
class(molecules)
## [1] "character"

The function str() provides an overview of the structure of an object and its elements. It is a useful function when working with large and complex objects:

str(weight_g)
##  num [1:4] 50 60 65 82
str(molecules)
##  chr [1:3] "dna" "rna" "protein"

You can use the c() function to add other elements to your vector:

weight_g <- c(weight_g, 90) # add to the end of the vector
weight_g <- c(30, weight_g) # add to the beginning of the vector
weight_g
## [1] 30 50 60 65 82 90

In the first line, we take the original vector weight_g, add the value 90 to the end of it, and save the result back into weight_g. Then we add the value 30 to the beginning, again saving the result back into weight_g.

We can do this over and over again to grow a vector, or assemble a dataset. As we program, this may be useful to add results that we are collecting or calculating.

A vector is the simplest R data type and is a linear vector of a single type. Above, we saw 2 of the 6 main vector types that R uses: "character" and "numeric" (or "double"). These are the basic building blocks that all R objects are built from. The other 4 vector types are:

  • "logical" for TRUE and FALSE (the boolean data type)
  • "integer" for integer numbers (e.g., 2L, the L indicates to R that it’s an integer)
  • "complex" to represent complex numbers with real and imaginary parts (e.g., 1 + 4i) and that’s all we’re going to say about them
  • "raw" for bitstreams that we won’t discuss further

You can check the type of your vector using the typeof() function and inputting your vector as the argument.

Vectors are one of the many data structures that R uses. Other important ones are lists (list), matrices (matrix), data frames (data.frame), factors (factor) and arrays (array).

► Question

We’ve seen that vectors can be of type character, numeric (or double), integer, and logical. But what happens if we try to mix these types in a single vector?

► Solution

► Question

What will happen in each of these examples? (hint: use class() to check the data type of your objects):

num_char <- c(1, 2, 3, "a")
num_logical <- c(1, 2, 3, TRUE)
char_logical <- c("a", "b", "c", TRUE)
tricky <- c(1, 2, 3, "4")

► Solution

► Question

Why do you think it happens?

► Solution

► Question

How many values in combined_logical are "TRUE" (as a character) in the following example:

num_logical <- c(1, 2, 3, TRUE)
char_logical <- c("a", "b", "c", TRUE)
combined_logical <- c(num_logical, char_logical)

► Solution

► Question

In R, we call converting objects from one class into another class coercion. These conversions happen according to a hierarchy, whereby some types get preferentially coerced into other types. Can you draw a diagram that represents the hierarchy of how these data types are coerced?

► Solution

3.5 Subsetting vectors

If we want to extract one or several values from a vector, we must provide one or several indices in square brackets. For instance:

molecules <- c("dna", "rna", "peptide", "protein")
molecules[2]
## [1] "rna"
molecules[c(3, 2)]
## [1] "peptide" "rna"

We can also repeat the indices to create an object with more elements than the original one:

more_molecules <- molecules[c(1, 2, 3, 2, 1, 4)]
more_molecules
## [1] "dna"     "rna"     "peptide" "rna"     "dna"     "protein"

Note: R indices start at 1. Programming languages like Fortran, MATLAB, Julia, and R start counting at 1, because that’s what human beings typically do. Languages in the C family (including C++, Java, Perl, and Python) count from 0 because that’s simpler for computers to do.

Finally, it is also possible to get all the elements of a vector except some specified elements using negative indices:

molecules ## all molecules
## [1] "dna"     "rna"     "peptide" "protein"
molecules[-1] ## all but the first one
## [1] "rna"     "peptide" "protein"
molecules[-c(1, 3)] ## all but 1st/3rd ones
## [1] "rna"     "protein"
molecules[c(-1, -3)] ## all but 1st/3rd ones
## [1] "rna"     "protein"

► Question

Here is another example of a character vector called fruits:

fruits <- c("apple", "orange", "grape")
  • add the elements melon and pineapple to this vector
  • sort them in alphabetic order
    • manually by using their index position,
    • and by using sort() (see ?sort).

► Solution

3.6 Conditional subsetting

Another common way of subsetting is by using a logical vector. TRUE will select the element with the same index, while FALSE will not:

weight_g <- c(21, 34, 39, 54, 55)
weight_g[c(TRUE, FALSE, TRUE, TRUE, FALSE)]
## [1] 21 39 54

Typically, these logical vectors are not typed by hand, but are the output of other functions or logical tests. For instance, if you wanted to select only the values above 50:

## will return logicals with TRUE for the indices that meet
## the condition
weight_g > 50
## [1] FALSE FALSE FALSE  TRUE  TRUE
## so we can use this to select only the values above 50
weight_g[weight_g > 50]
## [1] 54 55

You can combine multiple tests using & (both conditions are true, AND) or | (at least one of the conditions is true, OR):

weight_g[weight_g < 30 | weight_g > 50]
## [1] 21 54 55
weight_g[weight_g >= 30 & weight_g == 21]
## numeric(0)

Here, < stands for “less than”, > for “greater than”, >= for “greater than or equal to”, and == for “equal to”. The double equal sign == is a test for numerical equality between the left and right hand sides, and should not be confused with the single = sign, which performs variable assignment (similar to <-).

A common task is to search for certain strings in a vector. One could use the “or” operator | to test for equality to multiple values, but this can quickly become tedious. The function %in% allows you to test if any of the elements of a search vector are found:

molecules <- c("dna", "rna", "protein", "peptide")
molecules[molecules == "rna" | molecules == "dna"] # returns both rna and dna
## [1] "dna" "rna"
molecules %in% c("rna", "dna", "metabolite", "peptide", "glycerol")
## [1]  TRUE  TRUE FALSE  TRUE
molecules[molecules %in% c("rna", "dna", "metabolite", "peptide", "glycerol")]
## [1] "dna"     "rna"     "peptide"

► Question

Based on the height vector below, select heights that are above 190 or below or equal to 170

height <- c(163, 189, 210, 177, 168, 192, 170)

► Solution

► Question

Based on the fruits vector below:

  • subset the vector to only have melon and apple
  • test that orange is included in this vector and mango is not
fruits <- c("apple", "orange", "grape", "melon", "pineapple",
            "banana", "grape", "orange", "melon")

► Solution

► Question

Can you figure out why "four" > "five" returns TRUE?

► Solution

3.7 Names

It is possible to name each element of a vector. The code chunk below show a initial vector without any names, how names are set, and retrieved.

x <- c(1, 5, 3, 5, 10)
names(x) ## no names
## NULL
names(x) <- c("A", "B", "C", "D", "E")
names(x) ## now we have names
## [1] "A" "B" "C" "D" "E"

When a vector has names, it is possible to access elements by their name, in addition to their index.

x[c(1, 3)]
## A C 
## 1 3
x[c("A", "C")]
## A C 
## 1 3

3.8 Missing data

As R was designed to analyze datasets, it includes the concept of missing data (which is uncommon in other programming languages). Missing data are represented in vectors as NA.

When doing operations on numbers, most functions will return NA if the data you are working with include missing values. This feature makes it harder to overlook the cases where you are dealing with missing data. You can add the argument na.rm = TRUE to calculate the result while ignoring the missing values.

heights <- c(2, 4, 4, NA, 6)
mean(heights)
## [1] NA
max(heights)
## [1] NA
mean(heights, na.rm = TRUE)
## [1] 4
max(heights, na.rm = TRUE)
## [1] 6

If your data include missing values, you may want to become familiar with the functions is.na(), na.omit(), and complete.cases(). See below for examples.

## Extract those elements which are not missing values.
heights[!is.na(heights)]
## [1] 2 4 4 6
## Returns the object with incomplete cases removed.  The returned
## object is a vector of type `"numeric"` (or `"double"`).
na.omit(heights)
## [1] 2 4 4 6
## attr(,"na.action")
## [1] 4
## attr(,"class")
## [1] "omit"
## Extract those elements which are complete cases.  The returned
## object is a vector of type `"numeric"` (or `"double"`).
heights[complete.cases(heights)]
## [1] 2 4 4 6

► Question

  1. Using this vector of heights in inches, create a new vector with the NAs removed.
heights <- c(63, 69, 60, 65, NA, 68, 61, 70, 61, 59, 64, 69, 63,
             63, NA, 72, 65, 64, 70, 63, 65)
  1. Use the function median() to calculate the median of the heights vector.
  2. Use R to figure out how many people in the set are taller than 67 inches.

► Solution

3.9 Generating vectors

Constructors

There exists some functions to generate vectors of different type. To generate a vector of numerics, one can use the numeric() constructor, providing the length of the output vector as parameter. The values will be initialised with 0.

numeric(3)
## [1] 0 0 0
numeric(10)
##  [1] 0 0 0 0 0 0 0 0 0 0

Note that if we ask for a vector of numerics of length 0, we obtain exactly that:

numeric(0)
## numeric(0)

There are similar constructors for characters and logicals, named character() and logical() respectively.

► Question

What are the defaults for character and logical vectors?

► Solution

Replicate elements

The rep function allow to repeat a value a certain number of times. If we want to initiate a vector of numerics of length 5 with the value -1, for example, we could do the following:

rep(-1, 5)
## [1] -1 -1 -1 -1 -1

Similarly, to generate a vector populated with missing values, which is often a good way to start, without setting assumptions on the data to be collected:

rep(NA, 5)
## [1] NA NA NA NA NA

rep can take vectors of any length as input (above, we used vectors of length 1) and any type. For example, if we want to repeat the values 1, 2 and 3 five times, we would do the following:

rep(c(1, 2, 3), 5)
##  [1] 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3

► Question

What if we wanted to repeat the values 1, 2 and 3 five times, but obtain five 1s, five 2s and five 3s in that order? There are two possibilities - see ?rep or ?sort for help.

► Solution

Sequence generation

Another very useful function is seq, to generate a sequence of numbers. For example, to generate a sequence of integers from 1 to 20 by steps of 2, one would use:

seq(from = 1, to = 20, by = 2)
##  [1]  1  3  5  7  9 11 13 15 17 19

The default value of by is 1 and, given that the generate of a sequence of one value to another with steps of 1 is frequently used, there’s a shortcut:

seq(1, 5, 1)
## [1] 1 2 3 4 5
seq(1, 5) ## default by
## [1] 1 2 3 4 5
1:5
## [1] 1 2 3 4 5

To generate a sequence of numbers from 1 to 20 of final length of 3, one would use:

seq(from = 1, to = 20, length.out = 3)
## [1]  1.0 10.5 20.0

Random samples and permutations

A last group of useful functions are those that generate random data. The first one, sample, generates a random permutation of another vector. For example, to draw a random order to 10 students oral example, I first assign each student a number from 1 to then (for instance based on the alphabetic order of their name) and then:

sample(1:10)
##  [1]  9  4  7  1  2  5  3 10  6  8

Without further arguments, sample will return a permutation of all elements of the vector. If I want a random sample of a certain size, I would set this value as second argument. Below, I sample 5 random letters from the alphabet contained in the pre-defined letters vector:

sample(letters, 5)
## [1] "s" "a" "u" "x" "j"

If I wanted an output larger than the input vector, or being able to draw some elements multiple times, I would need to set the replace argument to TRUE:

sample(1:5, 10, replace = TRUE)
##  [1] 2 1 5 5 1 1 5 5 2 2

► Question

When trying the functions above out, you will have realised that the samples are indeed random and that one doesn’t get the same permutation twice. To be able to reproduce these random draws, one can set the random number generation seed manually with set.seed() before drawing the random sample.

  • Test this feature with your neighbour. First draw two random permutations of 1:10 independently and observe that you get different results.

  • Now set the seed with, for example, set.seed(123) and repeat the random draw. Observe that you now get the same random draws.

  • Repeat by setting a different seed.

► Solution

Drawing samples from a normal distribution

The last function we are going to see is rnorm, that draws a random sample from a normal distribution. Two normal distributions of means 0 and 100 and standard deviations 1 and 5, noted noted N(0, 1) and N(100, 5), are shown below

Figure 3.1: Two normal distributions: N(0, 1) on the left and N(100, 5) on the right.

Two normal distributions: *N(0, 1)* on the left and *N(100, 5)* on the right.

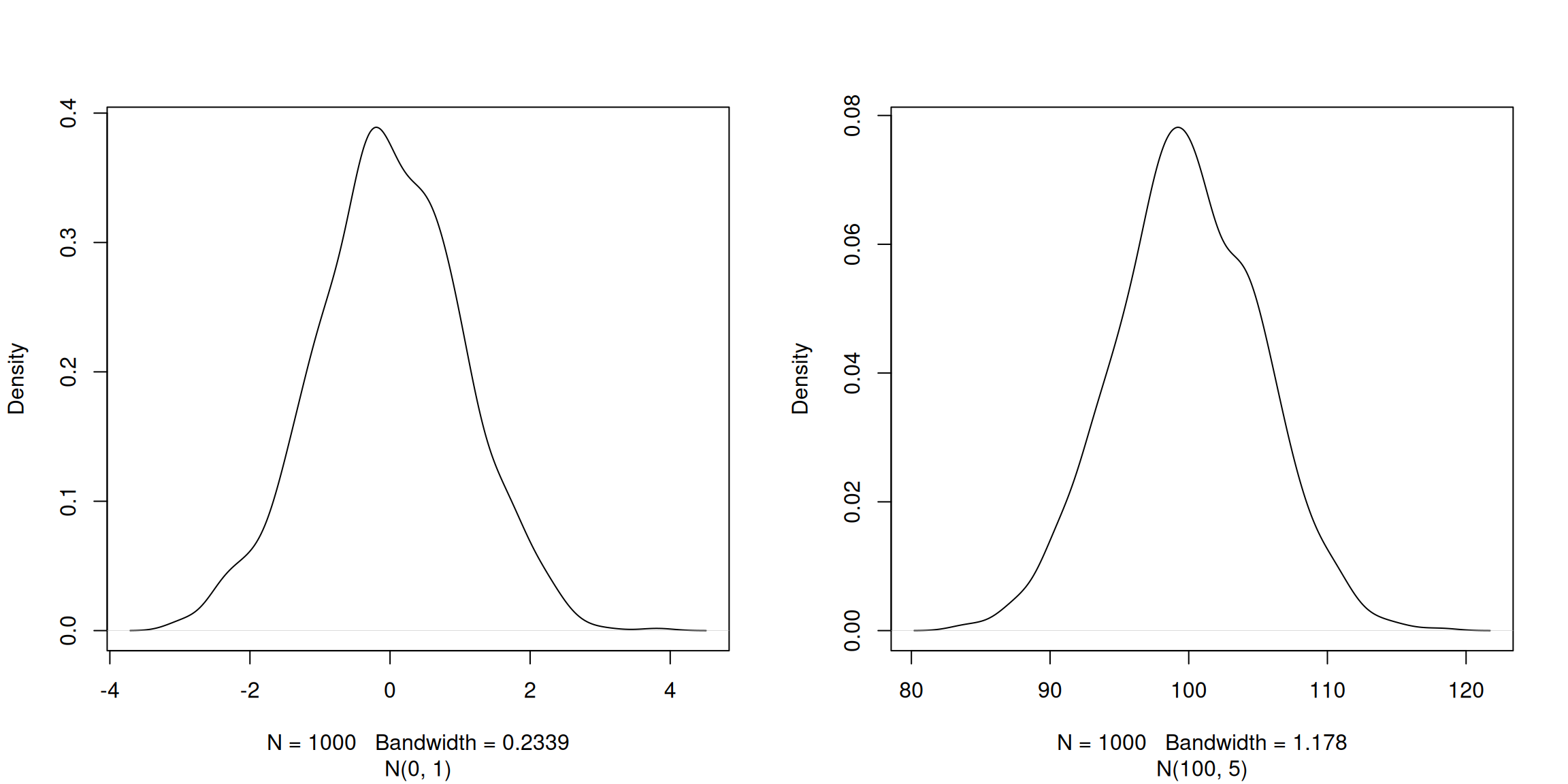
The three arguments, n, mean and sd, define the size of the sample, and the parameters of the normal distribution, i.e the mean and its standard deviation. The defaults of the latter are 0 and 1.

rnorm(5)
## [1]  0.69641761  0.05351568 -1.31028350 -2.12306606 -0.20807859
rnorm(5, 2, 2)
## [1]  1.3744268 -0.1164714  2.8344472  1.3690969  3.6510983
rnorm(5, 100, 5)
## [1] 106.45636  96.87448  95.62427 100.71678 107.12595

Now that we have learned how to write scripts, and the basics of R’s data structures, we are ready to start working with larger data, and learn about data frames.

3.10 Additional exercises

► Question

  • Create two vectors x and y containing the numbers 1 to 10 and 10 to 1 respectively. You can use the seq or : functions rather than constructing them by hand.
  • Check their type. Depending how they were created, they can be integers or doubles.
  • Take the sum (see the sum() function) of each vector and verify they are identical.
  • Sum vectors element-wise, and verify that all results are identical.
  • Swap the value or x and y.

► Question

  • Create a vector named x containing the numbers 20 to 2. Retrieve elements that are strictly larger than 5 and smaller or equal than 15.

  • Remove the first 8 elements from x and store the result in x2.

► Question

You’re doing an colony counting experiment, counting every day, from Monday to Friday how many molds you see in your cell cultures.

  • Create a vector named molds containing the results of your counts: 1, 2, 5, 8 and 10.

  • Set the names of molds using week days and extract the number of molds identified on Wednesday.

► Question

  • Calculate the mean of a random distribution N(15, 1) of size 100 and store it in variable m1.
  • Calculate the mean of a random distribution N(0, 1) of size 100 and store it in variable m2.
  • Calculate the mean of another random distribution N(15, 1) of size 1000 and store it in variable m3.
  • Can you guess which one of m1 and m2 will be larger? Verify in R.
  • Can you guess which one of m1 and m3 will be larger? Verify in R.

► Question

  • Using the sample function, simulate a set of 100 students voting (randomly) for 1, 2 or 3 breaks during the WSBIM1207 course.

  • Display the values as a table of votes.

  • Compute the number of students that wanted more that 1 break.

  • Bonus: as above, but setting the probability for votes to 1/5, 2/5 and 2/5 respectively. Read ?sample to find out how to do that.

► Question

Given vectors v1, v2 and v3 below

v1 <- c(1, 2, 3, "4")
v2 <- c(45, 23, TRUE, 21, 12, 34)
v3 <- c(v1, v2)
  • What is the class of v3?
  • What is the length of v3?
  • Assign names "a", "b", .. to the v3.
  • What is the value of v3["e"]?
  • Re-using v1, create a vector v4 containing
[1] "2"   "1"   "NEW" "3"   "4"
  • What is the command to round 3.1234 to two decimanl digits?
  • If you execute round(3.1234), you get 3. Why?

The WSBIM1207 students were asked how many breaks they wanted during the four-hour Thursday morning sessions. The answers are stored in vectors p1 (only one break of 30 minutes), p2 (two breaks of 15 minutes) and p3 (three breaks of 10 minutes).

p1 <- c(1, 1, 1)
names(p1) <- c("A34", "D3", "F12")
p2 <- c(2, 2, 2, 2)
names(p2) <- c("W4", "A21", "K7", "K8")
p3 <- c(3, 3, 3, 3, 3, 3, 3)
names(p3) <- c("D1", "D2", "A10", "D5", "D15", "A16", "B22")
  • What command would you use to identify the number of respective answers?
  • Concatenate all answers into a single vector p.
  • What command would you use to get the vote for student D2 from vector p?

► Question

Copy and paset the code chunk below to generate a vector of marks, including some students with missing values that didn’t take that test.

c(student1 = 12, student2 = 11, student3 = 4, student4 = 6, student5 = 7,
  student6 = 8.5, student7 = 13.5, student8 = 5.5, student9 = 13.5,
  student10 = 2.5, student11 = 17, student12 = 18, student13 = 15,
  student14 = 8, student15 = 7, student16 = 12, student17 = 18.5,
  student18 = 7.5, student19 = 13.5, student20 = 6, student21 = 9,
  student22 = 16, student23 = 8.5, student24 = 9, student25 = NA,
  student26 = NA, student27 = 14, student28 = 16.5, student29 = 12,
  student30 = NA, student31 = 12.5, student32 = 3, student33 = NA,
  student34 = 17, student35 = 16, student36 = 9, student37 = 6,
  student38 = 7, student39 = 8.5, student40 = 8.5, student41 = 8,
  student42 = 16.5, student43 = 4.5, student44 = NA, student45 = 8,
  student46 = 8, student47 = 7.5, student48 = 8.5, student49 = 2,
  student50 = 14, student51 = 6.5, student52 = 12, student53 = 16.5,
  student54 = 7, student55 = 9.5, student56 = 12, student57 = 8.5,
  student58 = 15.5, student59 = 9, student60 = 13.5, student61 = 18,
  student62 = 12.5, student63 = 19.5, student64 = 13, student65 = 17.5,
  student66 = 8.5, student67 = 9, student68 = 7, student69 = 12.5,
  student70 = NA, student71 = 19, student72 = 11.5, student73 = 9,
  student74 = 9.5, student75 = 12, student76 = 11, student77 = 12,
  student78 = 14, student79 = 17, student80 = 8.5, student81 = 10,
  student82 = 10, student83 = NA, student84 = 10.5, student85 = 14,
  student86 = 7.5, student87 = 4, student88 = 9, student89 = 6.5,
  student90 = 10.5, student91 = 9.5, student92 = 13, student93 = 11.5,
  student94 = NA, student95 = 6, student96 = 12.5, student97 = 11.5,
  student98 = 4, student99 = 11.5, student100 = 8)

  • What is the number of students that have a mark > 10?

  • What is the number of students that have a mark greater than the average score?

Page built: 2024-08-27 using R version 4.4.1 (2024-06-14)